Joint Research Group Theory of Electron Dynamics and Spectroscopy
Research history
Silicon-Based Molecule and Polymer Chemistry
Silicon, a forth main group element, can partly or fully substitute tetra-bonded carbon in organic molecules.Already in the case of a single substitution of carbon with silicon, the change of the electronic structure can have a strong effect on the reactivity of the molecule. One of the responsible properties is the reduced electronegativity of silicon compared to carbon. Therefore, with a suitable catalyst, hydride transfer to an organic hydride acceptor, i.e. a reduction, becomes possible. An interesting special case ist the Lewis- or Brønsted acid catalyzed reductive ether formation of carbonyl compounds [1].

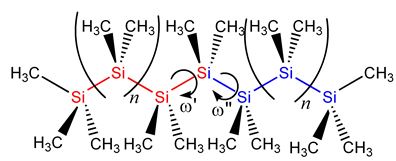
In the case of silanes, silicon organic compounds analogous with alcanes, completely new properties appear, that make silanes chemically, physically, and technologically outstanding. For example does the red shift of the UV excitation in planar, permethylated silanes upon chain lengths extension go back to the exceptional delocalization of σ-electrons along the silane backbone. Systematic studies on the dependency of the σσ* excitation energy on the dihedral angles let to the cognition, that the σ-delocalization in permethylated oligosilanes of varying lengths has its minimal effect for small angles of 15-30° [2]. Currently the absorption spectra of helical peralkylated oligosilanes of different lengths and helical tightness have been calculated in agreement with experiment and the nature of the transitions was analyzed [3].
[1] G. L. Larson, J. L. Fry, Ionic and Organometallic-Catalyzed Organosilane Reductions (John Wiley & Sons 2010).
[2] A. Bande, J. Michl, Chem. Eur. J. 15, 8504-8517 (2009) DOI:10.1002/chem.200901521.
[3] M. Jovanovic, D. Antic, D. W. Rooklin, A. Bande, J. Michl, Chem. Asian J. 12, 1250 (2017). DOI: 10.1002/asia.201700226.
Design of Novel Functional Materials
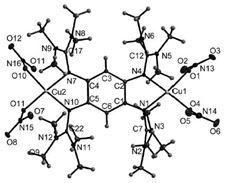
The presently investigated functional materials are aromatic conductive coordination polymeres of the family of guanidyl functionalised aromatic systems (GFAs) [1] that are potential elecron donors and redox active ligands. For selected monomers the structure property relation in GFA ligands and complexes is investigated.
[1] C. Trumm et al., Eur. J. Inorg. Chem. 3102-3108 (2010); D. Emeljanenko et al., Eur. J. Inorg. Chem. 1839-1846 (2010).
Quantum Monte Carlo
The quantum Monte Carlo (QMC) method is one of the modern methods for electron structure calculations, that directly incorporates electron correlation. The latter is treated explicitly, because the electronic many-particle problem is solved as such, whereas orbital or density functional based standard approaches reduce it to coupled problems of one electron in the mean field of the others. In the many-particle treatment it is essential to fulfill the cusp condition at the coalescence points of nuclei and electrons and of two electrons, respectively, which is possible with an explicitly correlated wave function (e.g. of Jastrow type). The solution of the Schrödinger equation is obtained in a Markow random walk process for either numerical integration in variational QMC (VMC) or propagation in imaginary time in diffusion QMC (DMC), where the latter is the more accurate method [1].
For the calculation of transition metals, the many-particle problem is already too complex, to allow a description of core and valence electrons at the same level of accuracy. Furthermore, relativistic effects gain importance. Therefore, effective core potentials are used in the basis set. In vanadium oxide cluster calculations as one of the first QMC calculations on transition metal compounds, it could be shown, that the strategy to use scalar relativistic effective core potentials let to accurate and stable DMC calculations [2,3].
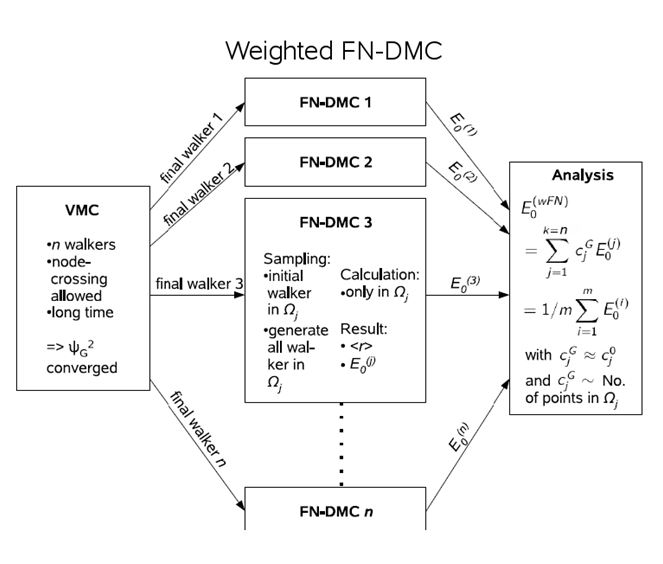
A famous problem of DMC is the so-called node problem, where nodes refer to the zeros of the wave function. A many-particle wave function already has a complicated nodal structure due to the Pauli principle. In excited states, further nodes appear. The random walk in DMC takes effectively place in one pocket between the nodes, which is no problem as long as all those pockets are identical. This is the case for accurate ground state wave functions. However, it has not been proven for excited states. To obtain accurate results with reduced nodal error, the nodal pockets needs to be populated initially according to the VMC electron density. Then several DMC calculations with that occupation need to be performed and the results are averaged. This methodology is termed weighted DMC and has successfully been applied to Rydberg states of the C atom and CO [2,4,5]. [1] B. L. Hammond, W. A. Lester, Jr., P. J. Reynolds, Monte Carlo Methods in Ab Initio Quantum Chemistry (World Scientific, Singapore, 1994).
[2] A. Bande, Dissertation, RWTH Aachen University, Aachen (2007) URL.
[3] A. Bande, A. Lüchow, Phys. Chem. Chem. Phys. 10, 3371-3376 (2008) DOI:10.1039/B803571G.
[4] A. Bande, A. Lüchow, F. Della Sala, and A. Görling, J. Chem. Phys. 124, 114114, 1-6 (2006) DOI:10.1063/1.2180773.
[5] A. Bande, A. Lüchow, in Advances in Quantum Monte Carlo, ed.: J. B. Anderson, S. M. Rothstein (American Chemical Society, Washington, DC, 2007) pp 42-54, DOI:10.1021/bk-2007-0953.ch004.
Exact Solution of the Schrödinger Equation
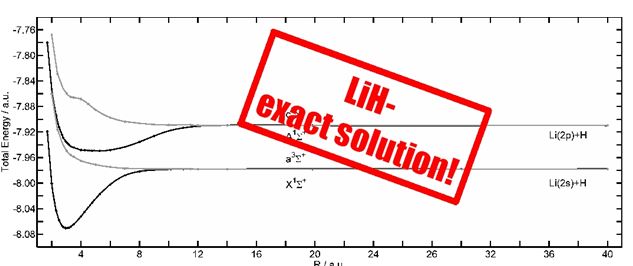
The common electronic structure methods are all approximative methods to solve the time-independent Schrödinger equation, for which analytic solutions exist only for few, small systems, e.g. the Hydrogen atom. Recently, it has been shown, that it is possible to analytically generate a flexible atomic or molecular wave function, which converges to the exact eigenfunction. It is generated by repeated operation of the Hamiltonian on an initial wave function. This procedure is based on the theorem, that the solution of the Schrödinger equation must be a function of the Hamilton operator [1]. In the Free Complement Local Schrödingr Equation (FC LSE) method, the integrals, that lead to the solution, i.e. the coefficients of the wave function and the corresponding energies, are evaluated in a random walk process [2]. For LiH, most accurate potential energy surfaces have been obtained using this ansatz [3]. Similarly, LiH can be calculated without the Born-Oppenheimer approximation.
[1] H. Nakatsuji (et al.): J. Chem. Phys. 113, 2949 (2000) DOI:10.1063/1.1287275; J. Chem. Phys. 115, 2000 (2001) DOI:10.1063/1.1383032; Phys. Rev. Lett. 93, 030403 (2004) DOI:10.1103/PhysRevLett.93.030403
[2] H. Nakatsuji, H. Nakashima, Y. Kurokawa, A. Ishikawa, Phys. Rev. Lett. 99, 240402 (2009) DOI:10.1103/PhysRevLett.99.240402.
[3] A. Bande, H. Nakashima, and H. Nakatsuji, Chem. Phys. Lett. 496, 347-350 (2010) DOI:10.1016/j.cplett.2010.07.041.